Successful Project Management

by Tyrone "let's just polish that 17th decimal place" White
Tyrone has his own style of project management based on an ancient principle of work management developed by the Roman civil servant Guyus Chilloutus.  The theory has since been given the name of 'Extended Theory of Employment Related to Near Asymptotic Limits' or 'ETERNAL' for short.

The basic tenets of the theory are (as adapted by Tyrone):
   
  • Never complete a project until either the money has run out or it's no longer cool to be working on it.
     
  • Always have a very complex diagram you can put in front of someone so that they think that you must be doing a really good job.
  • Always have at least fifteen extra things you need to do before the project will be completed.
     
  • If things are getting too intense, cruise the office and talk to the guys and gals.
     
  • Never put 'Final' on anything.
It is worth noting that Roman historian Flavius Eutropius blamed ETERNAL for the collapse of the Roman Empire and subsequent rule of Europe by barbarians.
   
Modern mathematical analysis has allowed the theory to be placed on a more definitive grounding.  Much of this work was carried out by A. Wiles following the rather simpler task of proving Fermat's Last Theorem.  What we show here is just a brief overview.
   
The graph shown here illustrates the ideal ETERNAL project completion chart. In this case, the completion factor C is given by:

 

   
where is d a time constant that is dependent on the planned duration and whether the project is reimbursable or not. (It should be noted that this ignores the initial 'forming' stage of the project where not much progress is made "cos you've got to hang out with the guys".)

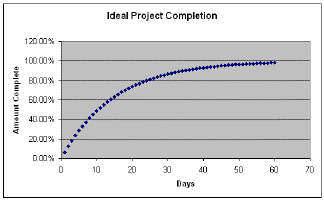
Though this basic theory provides a good approximation for most of the duration of a project, the really difficult bit comes in the tricky 'near-end' phase.  Here we have to define the 'Limits' where project termination becomes unavoidable.  Again these are dependent on the type of project (reimbursable, fixed price etc), but require a mathematical definition of events such as:

  • When the customer says 'You've spent how much!' (this is specific to reimbursable contracts)
  • When the accuracy of the answer has reached the number of decimal places on your calculator
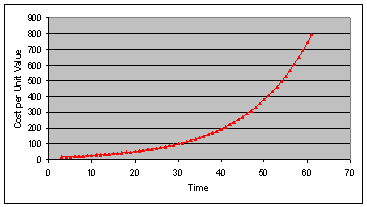
  • When the cost per unit value for the customer exceeds the GNP of a small country (reimbursable contracts again)

This last point is illustrated in the graph below, where, as the progress asymptotes to 100% and the expenditure remains constant, the cost per unit value increases exponentially
 

 
In order to correct for this, the 'Tee' factor was introduced.  In this, the exponential growth in cost per unit value is counteracted by working ever longer hours.  However, this can only be a temporary correction, even if more members of the team are dragged in, as the number of hours required per day eventually reaches 24.  This is often the event that forces project termination.

By combining the 'Tee' factor with 'Disaster Theory' and 'Chaos Theory' the underlying mathematical support for ETERNAL has been developed. Now known as the 'Bugger, is That the Time? Conjecture', it gives us the ultimate project delivery mechanism

   
Further reading:  'The Decline and Fall of the Roman Empire', Gibbon, Edward (1737-1794)
   
(The reader should not confuse ETERNAL with U-TURN, a management philosophy utilised in many technology organisations)